איך עובדים אמצעי חיכוך?
תוכן עניינים
מאמר בעבודה!
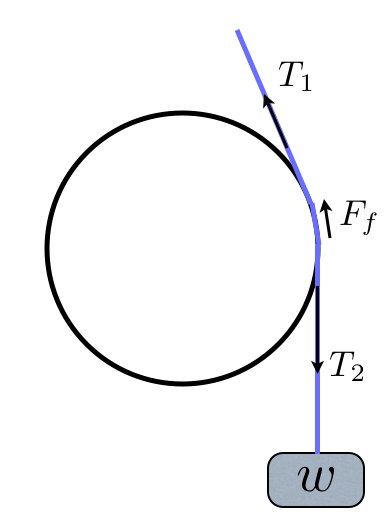
רובם המכריע של אמצעי החיכוך פועלים על פי עיקרון אחד, שמודגם יפה על ידי חבל המלופף על תוף. הרעיון של אמצעי החיכוך הוא לגרום לחבל להפעיל כוח בניצב לאביזר, וכך ליצור כוח חיכוך. ככל שהחיכוך גדול יותר, כך נדרש להפעיל פחות כוח בהחזקת החבל. הדרך לעשות זאת היא ליצור "שבירה" של החבל סביב משהו: תוף, טבעת, עמוד, אמצעי חיכוך.
אותו עיקרון פועל גם לאורכו של חבל המתחכך בסלע.
תזכורת בענייני חיכוך, וחישוב פשוט
תזכורת קצרה: כוח החיכוך ניתן על ידי: [math]F_f=\mu F_N[/math]. כאשר: [math]\mu[/math] נקרא מקדם החיכוך והוא תכונה של שני החמרים של הגופים הבאים במגע, ו [math]F_N[/math], הכוח הנורמלי, הוא הכוח הניצב למישור המגע בין שני הגופים.
כדי להבין את המשך המאמר אין צורך להתעמק בפיתוח המתמטי-פיזיקלי. המאותגרים מתמטית מוזמנים לקחת את הנוסחה הסופית, ולדלג על החישובים, ישר לדוגמאות.
נסתכל על כוח החיכוך על אלמנט אורך חבל על תוף:
כשאלמנט אורך (קטע קצר) של חבל עובר על חלק של תוף עגול, ניתן לחשב בקלות את החיכוך על ידי הנוסחה הרגילה. נניח שהקטע שנוגע בחבל הוא כלכך קצר, שהוא בקירוב ישר. הציור מתאר את הכוחות הפועלים עליו:
הכוח הנורמאלי [math]F_N[/math] הוא פעמיים הרכיב של המתיחות [math]T[/math] בכיוון מרכז התוף. רכיב זה מסומן [math]T_y[/math], והוא שווה ל:
[math]T_y=\mu T\sin\frac{\alpha}{2}[/math]
ולכן כוח החיכוך הוא:
[math]F_f=\mu F_N=2 \mu T_y\,\![/math]
או, בהצבה של [math]F_N[/math]:
[math]F_f=2\mu T \sin\frac{\alpha}{2}[/math]
כוח החיכוך מתנגד להחלקה של החבל על התוף, ולמעשה המתיחויות בשני צידי התוף אינה זהה. התמונה הבאה היא יותר אמיתית:
המתיחות בחבל הקרוב למשקולת, הוא המשקל, לכן: [math]T_2=w[/math].
המתיחות אחרי התוף קטנה יותר, ומסומנת כאן [math]T_1[/math].
כוח החיכוך, [math]F_f[/math], תלוי בכוח הנורמאלי, [math]F_N[/math], שאותו כבר מצאנו.
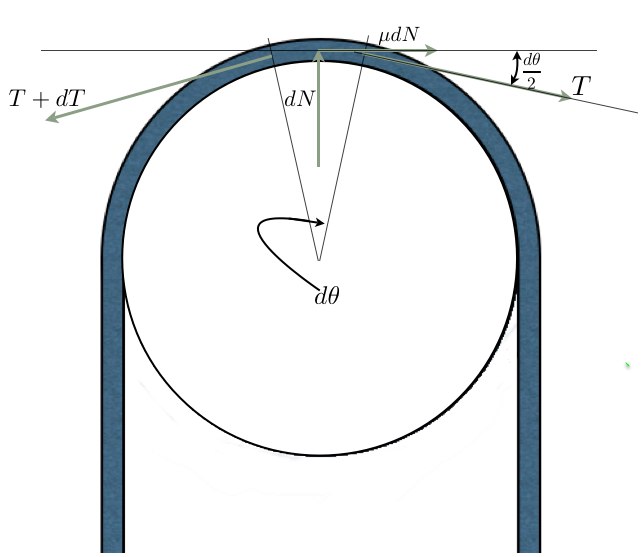
כשקטע ארוך יותר של חבל עובר על התוף, המתיחות משתנה עם כל אלמנט חבל. שינוי המתיחות [math]dT[/math], מתרחש עם כל שינוי של [math]d\alpha[/math] בזווית. נסמן את הכוח הנורמלי שמפעיל אלמנט חבל זה ב[math]dN[/math]. כוח החיכוך הוא הסכום של שינוי המתיחויות (למעשה - אינטגרל) על כל אלמנטי האורך של החבל המתחככים בתוף.
במצב שיווי משקל, סכום הכוחות מתאפס, בפרט גם סכום הכוחות בכיוון [math]x[/math]:
[math]\Sigma F_x=0\,\![/math]
[math]T\cos\frac{d\theta}{2}+\mu(dN)-(T+dT)\cos\frac{d\theta}{2}=0[/math]
מכיוון ש [math]d\theta^2[/math] הוא קטן מאד, והקוסינוס שלו הוא אחד, הביטוי מצטמצם ל:
[math]\mu(dN)=dT\,\![/math]
בדומה, הכוחות בכיוון y, מתאפסים ומן האילוץ [math]\Sigma F_y=0\,\![/math], מקבלים:
[math]dN-(T+dT)\sin\frac{\theta}{2}+T\sin\frac{\theta}{2}=0[/math]
משיקולים דומים (סינוס של ביטוי קטן מאד הוא אפס), הביטוי מצטמצם ל:[math]dN=Td\theta\,\![/math]
אם נציב את [math]dN[/math], נוכל לקבל ביטוי שאינו תלוי בכוחות הנורמאליים והוא משוואה דיפרנציאלית המבטאת את [math]T[/math]:
[math]\frac{dT}{T}=\mu d\theta\,\![/math]
כדי לקבל את ההפרש במתיחות בין הצדדים, יש לסכום (לאנטגרל) על זווית המגע הכללית בין החבל לבין התוף:
[math]\int_{T_1}^{T_2}\frac{dT}{T} = \int_0^\alpha \mu d\theta[/math]
ואינטגרציה נותנת:
[math]\ln\frac{T_1}{T_2} = \mu\alpha[/math]
הכוח בו צריך למשוך את החבל בצד השני של התוף [math]T_1[/math] הוא:
[math]T_2=T_1e^{\mu\alpha}\,\![/math]
וכוח החיכוך הוא ההפרש בין המתיחויות בחבל בשני צידי התוף:
[math]F_f=T_2(1-e^{\mu\alpha})\,\![/math]
סיכום ביניים
קיבלנו כי לאורך החבל המתחכך בתוף, אין השפעה על החיכוך (ולכן אין השפעה לקוטר התוף). אין תלות באורך, ולא בשטח המגע עם התוף, ובכך זה דומה לחיכוך של גוף המחליק על משטח.
החיכוך מושפע משלושה גורמים:
- המתיחות בחבל.
- מקדם החיכוך בין החבל והתוף.
- זוית המגע (חלק הסיבוב) שעובר החבל סביב התוף (למעשה, זה נכון בתוף מקוטר מסויים ומעלה, אבל זה קירוב טוב).
החיכוך תלוי באופן ישר במתיחות, ועולה אקספוננציאלית עם זווית המגע ועם מקדם החיכוך.
חשוב לזכור שמקדם החיכוך תלוי במידה רבה במצב החבל ובתכונותיו. עבור חבל חדש, ועוד יותר מכך, חבל רטוב או מבוצבץ, מקדם החיכוך יהיה נמוך. לחבל בלוי ו"צמרי", יהיה מקדם חיכוך גבוה.
עניין אחרון, הזווית [math]\alpha[/math] במשוואה, היא ביחידות של רדיאנים. אם רוצים להציב ערכים ולקבל תוצאה מספרית, אלו היחידות בהן צריך להשתמש.
נזכיר כי רדיאן אחד הוא הזווית בה אורך הקשת שווה לרדיוס. מכיוון שהיחס בין הרדיוס להיקף הוא [math]2\pi[/math], הרי שזווית המגע על פני סיבוב שלם, 360°, היא [math]2\pi[/math] רדיאנים, או 6.28 רדיאנים, בערך. רדיאן אחד שווה ל-57.29°.
דוגמה1: מוט עגול, צינור או טיובה
דוגמה2: סולם
דוגמה3: שמינית
אם בוחנים את מעבר החבל בשמינית מגלים שבמצב בו יש מינימום חיכוך, שבו "קל" לתת חבל, יש זווית מגע של 540°. במצב "נעול", כלומר עם חיכוך מקסימאלי ולכל היותר, זווית
קישורים חיצוניים
תרמו לדף זה: מיכה יניב ואחרים...